El mago japonés de las matemáticas exhibe sus trucos en Madrid

“Soy un matemago”. Así se presenta Jin Akiyama cada vez que muestra su espectáculo de matemáticas y magia en escenarios de todo el mundo. Este jueves lo ha hecho en Madrid ante una sala abarrotada de público en la Residencia de Estudiantes, organizadora del evento junto al CSIC y el Instituto de Ciencias Matemáticas (ICMAT).

Akiyama es profesor en la Universidad de Ciencias de Tokio, pero además, desde hace dos décadas conduce un programa de máxima audiencia sobre matemáticas en la televisión nipona, por lo que es todo un experto en la divulgación de esta materia al gran público.

“Las matemáticas son una herramienta muy poderosa para hacer posible lo imposible, con muchos aspectos y aplicaciones que conviene dar a conocer a la gente”, destaca a Sinc la estrella mediática que, en esta ocasión, comenzó su espectáculo con uno de sus números favoritos: la construcción de un puzle a partir de un tetraedro.

Recortando una pirámide hueca formada por varias capas –tantas como se quiera–, el profesor generó una sola figura plana, separó las capas y sorprendentemente todas encajaban perfectamente como las piezas de un rompecabezas. Incluso aunque creara figuritas con forma de burros, todas se ajustaban perfectamente. La sala rompió en aplausos.

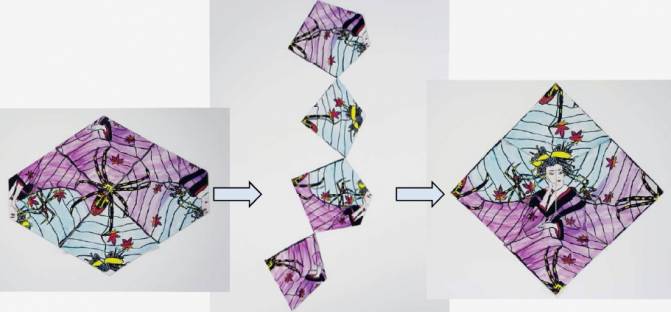
La araña del hexágono se transforma en la geisha del cuadrado. / J. Akiyama

Después, para ilustrar el concepto de cambio o transformación, un fenómeno habitual en la naturaleza –como el paso de líquido a sólido o las modificaciones que sufren los cristales–, el matemago puso dos ejemplos. Uno con una figura que podía ser tanto un conejo como un pato, dependiendo de la perspectiva, y otro con una tela de araña dibujada en un hexágono que al mover sus piezas se transformaba en una bella geisha encerrada en un cuadrado.

Muchas matemáticas detrás del espectáculo

Diversos experimentos con poliedros ayudaron a observar cómo estos sólidos también mantienen su volumen aunque cambien de aspecto de forma sorprendente. Así, un octaedro truncado apretado en un cubo puede hacer hueco a otro igual si se distribuyen bien sus partes. Y lo que dejó perpleja a la audiencia fue ver cómo otro octaedro de este tipo pintado de cerdito se convertía en un gran 'taco' de jamón; o de modo similar, un dodecaedro rómbico con aspecto de zorro pudo revertirse en una serpiente cuboide verde.

El zorro del dodecaedro rómbico es engullido por la serpiente cuboide. / J. Akiyama

“Es una manera muy didáctica y atractiva de presentar los experimentos, sobre todo para la gente más joven, pero no hay que olvidar que hay muchas matemáticas detrás de este espectáculo”, recordaba el director del ICMAT, Manuel de León, que fue el testigo solicitado por Akiyama para verificar cómo aunque se raye un CD con un destornillador se sigue oyendo su música gracias al sistema de corrección de errores que lleva incorporado.

Para ejemplificarlo, el profesor japonés puso a prueba a los espectadores con un ejercicio en el que debían pensar un número e indicar si figuraba en una serie de conjuntos. Se permitía mentir una vez –como si fuera un error– y aun así el matemago siempre descubría el número elegido.

Akiyama también ha inventado máquinas increíbles, como taladros que hacen agujeros cuadrados e, incluso, triangulares y hexagonales. “Tengo la patente, pero nadie se ha interesado todavía”, bromeó mientras hacía una demostración con su artilugio.

Máquina que taladra agujeros cuadrados. / J. Akiyama

Más en serio, el matemático comentó, que aunque parezca que hacer orificios cuadrados o hexagonales no tiene sentido, puede ser relevante en tareas tan importantes como la retirada de las barras de combustible radiactivo de la central de Fukushima, ya que tienen esa forma.

Otro aspecto aplicado que escenificó fue la base matemática que está detrás de la eliminación de las piedras del riñón. En esencia se trata de una elipse con dos focos. En uno se sitúa la piedra del paciente y en el otro el doctor, que la bombardea con ondas ultrasónicas aprovechando la forma elipsoidal del aparato.

El profesor recomienda a sus colegas de colegios e institutos destacar estos aspectos aplicados cuando impartan la asignatura en sus clases: “Hay que enseñar lo importante que son las matemáticas en la vida diaria”. Y a los estudiantes los anima a que, "aunque al principio puedan resultar aburridas, gradualmente se pueden hacer más atractivas según se van estudiando y practicando”.

Con películas de jabón

Así lo demostró en la conferencia. Si hay un experimento que puso a prueba el ingenio del público fue averiguar la red mínima que se puede establecer entre varios puntos. Si solo hay dos es muy fácil: una recta. ¿Pero qué ocurre si son tres? ¿Cómo se pueden unir con la menor longitud posible? ¿Y si son cuatro, cinco o seis? Para resolverlo, el ponente contó con un aliado inesperado: las pompas de jabón.

El agua jabonosa detecta la red mínima entre tres, cuatro, cinco y seis puntos. / J. Akiyama

Mediante unos discos de metacrilato sumergidos en el agua jabonosa fue apareciendo de forma ‘mágica’ la red mínima que se crea entre tres puntos –tiene forma de Y–, cuatro –una especie de H–, cinco –una W con ‘patas’– y así sucesivamente. “La mayoría de la gente piensa que las matemáticas no tienen nada que ver con los experimentos, pero a veces también se hace uso de ellos”, dice Akiyama, que recientemente ha creado un centro en su universidad precisamente para experimentar e investigar con esta disciplina.

El profesor también enseñó cómo se pueden generar balones de fútbol y otros sólidos simplemente reflejando una imagen plana en espejos, así como el efecto de la rotación de una circunferencia en otra, o la manera de demostrar el teorema de Pitágoras con tres elefantes de madera. Su actuación terminó con todo el público trenzando dos corazones a partir de un par de cintas de Möbius.

Demostración del teorema de Pitágoras con tres elefantes. / J. Akiyama

Otro matemago, el español Fernando Blasco, profesor de Matemática Aplicada en la Universidad Politécnica de Madrid, destacó durante la presentación del acto que llevaba diez años esperando esta conferencia, ya que fue entonces cuando Akiyama vino a España con la intención de enseñar su espectáculo, pero le retuvieron todos sus materiales en el aeropuerto de Barajas. Afortunadamente pudo improvisar con un acordeón. En julio de 2015 el profesor japonés asistirá a un congreso en Barcelona, en la Universidad Politécnica de Cataluña, y confía en no tener problemas en El Prat.