Una treintena de divulgadores está organizando multitud de actividades en este ‘Marzo, mes de las Matemáticas’, con un acto central el Día de Pi (mes 3, día 14). Aquí van algunos ejemplos de las infinitas posibilidades que ofrecen los números, las figuras geométricas y otros entes matemáticos.
Durante este mes se está celebrando el mayor evento de divulgación de las matemáticas en España: Marzo, mes de las Matemáticas, promovido por la Red de Divulgación Matemática (DiMa) y financiado por la Fundación Española para la Ciencia y la Tecnología (FECYT).
Exposiciones, talleres, escape rooms, magia, cine, humor, cuentos, curiosidades, monólogos... La oferta es amplia para los amantes de las mates, que también podrán asistir a través de Youtube a la gran fiesta de este domingo 14 de marzo, Día de Pi y Día Internacional de las Matemáticas.
Además de para avanzar hacia un mundo mejor (como reza el eslogan de la iniciativa), esta ciencia despierta la lógica y ayuda a razonar. Para demostrarlo, cinco miembros de la DiMa nos retan con algunos ejercicios e historias.
Por Clara Grima, doctora en Matemáticas, profesora de la Universidad de Sevilla, divulgadora, autora del blog Mati y sus Mateoaventuras y varios libros.
La caja 'masu' es cuadrada, sin tapa y se usaba tradicionalmente en Japón para medir las cantidades de arroz. / Ilustración de Raquel Gu
Mi divulgador favorito de Matemáticas es japonés, Jin Akiyama, y este amigo me contó cómo hacer mediciones exactas con una caja de madera en la que no hay ninguna marca para orientarnos con la medida. La caja en cuestión se llama masu, es cuadrada y sin tapa. Se usaba tradicionalmente en Japón para medir cantidades de arroz, pero hoy algunas más pequeñas se utilizan para beber sake o poner sal, pimienta o especias.
El reto es el siguiente: tenemos un masu con 6 litros de capacidad y queremos usarlo para sacar agua de un recipiente y venderla, pero nuestros clientes (que llegan con un masu como el nuestro) solo nos piden cantidades enteras (1, 2, 3, 4, 5 o 6 litros, no vale litro y medio). Solo podemos coger agua del depósito una vez, aunque sí podemos devolverla cuantas veces queramos.
¿Cómo hacemos si el primer cliente nos pide 1 litro? Si llenamos el masu en el depósito, y vaciamos el agua hasta que quede alineada con dos de los vértices de la base, lo que nos queda es, exactamente, un litro, como en este dibujo:
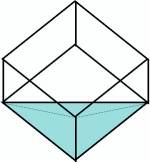
Si no me creen les recuerdo que el volumen de una pirámide, que es la figura que forma el agua, es:
Volumen pirámide = 1/3 [Base pirámide x Altura pirámide]
Como la altura de la pirámide es igual que la altura del masu y la base de la pirámide es la mitad de la base de la caja japonesa, tenemos que el volumen de nuestra pirámide de agua es el del masu (6 litros) dividido entre 6: exactamente 1.
Volumen pirámide = 1/3 [1/2(Base masu) x Altura masu] = 1/6 Volumen masu
¿Y si el cliente quiere 2 litros? Alguien podría pensar en repetir el método anterior dos veces, pero, no se puede. Solo podemos coger agua del depósito una vez. Vamos a ver primero cómo conseguir 3 litros con el masu y después, conocido esto, cómo sacar 2. Para medir 3 litros con nuestra caja solo tenemos que llenarla en el depósito y a continuación, vaciarla inclinándola hasta hacer coincidir el agua con una de las aristas del fondo de la misma, como en este dibujo:
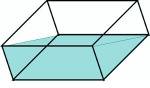
Luego, para medir 2 litros cogemos el masu lleno, con 6 litros, vaciamos 3 en el depósito alineando el agua con un lado de la caja. Nos quedan 3 litros en nuestra caja. Ahora volcamos el agua en el masu del cliente hasta que nos quede 1 en el nuestro como ya sabemos, alineando con los vértices. Le habremos puesto 2 al cliente y el que sobra, de vuelta al depósito.
¿Y 4 litros? Tomamos 6 del depósito, soltamos 3 en el masu del cliente como antes, alineando con el lado, volcamos nuestro masu en el depósito hasta dejar solo 1 litro alineando con los vértices y se lo echamos al cliente. Y vender 5 litros es muy fácil: basta llenar nuestro masu con 6 litros y vaciar el agua en el del cliente hasta que en el nuestro solo quede 1.
Por Sergio Belmonte, vicepresidente del Museu de Matemàtiques de Catalunya, autor del blog Magiaymatematicas y profesor de Secundaria en un instituto donde utiliza la gamificación para enseñar matemáticas.
Ejercicio sobre 'Exploding dots'. / Global Math Project
El recurso didáctico de los Exploding dots (puntos explosivos) nos ofrece una representación gráfica, divertida y muy visual de los sistemas de numeración, de la aritmética y del álgebra básica. Para esta representación se utilizan 'máquinas' con cajas donde se introducen 'puntos' que explotan de una manera particular, operando de derecha a izquierda.
Por ejemplo, una máquina 1 ← 2 (leída al revés, dos-uno) cada vez que encuentra dos puntos en una caja los hace explotar y los convierte en un solo punto en la caja que hay inmediatamente a su izquierda, como vemos aquí:
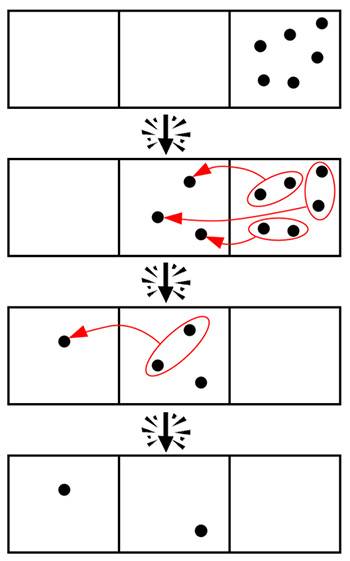
Así se pueden transformar puntos en códigos de 0 y 1. En este ejemplo, la distribución final de las cajas (un punto, un punto, cero puntos) sería convertida en el código 110 por la máquina.
En este vídeo podemos ver la máquina en acción. A ver si resuelves (sin mirar las respuestas en los comentarios) la incógnita que se plantea al final.
Estas máquinas se pueden utilizar para navegar por los diferentes sistemas de numeración, tipos de números (naturales, enteros, decimales, etc…), operaciones e incluso los primeros conceptos de álgebra. El límite lo pondrá vuestra imaginación.
Se trata de una alternativa a los métodos de cálculo tradicionales y también una nueva manera de introducirlos en clase que facilita su comprensión y posterior asimilación por parte del alumnado, un recurso con muchas posibilidades por descubrir.
Los Exploding dots es una propuesta de James Tanton dentro del Global Math Project que se organiza cada año para estudiantes de todo el mundo. El año pasado participaron casi 7 millones. Tan sólo se necesita lápiz y papel para poder empezar a disfrutar de este fantástico recurso.
Por Marta Macho, profesora en la Universidad del País Vasco, divulgadora del papel de la mujer en la ciencia e incansable luchadora por la igualdad de género. Participa en la web Mujeres con ciencia.
Esther Szekeres (Klein de familia), Paul Erdös y George Szekeres, protagonistas de esta historia muchos años después. / ©The University of Newcastle/UON Photographer
Esta historia la protagonizaron tres famosos matemáticos húngaros en su juventud. En el invierno de 1933, un pequeño grupo de estudiantes se reunía en algún lugar de Budapest para hablar de matemáticas. Entre ellos se encontraban Paul Erdős, Esther Klein y George Szekeres.
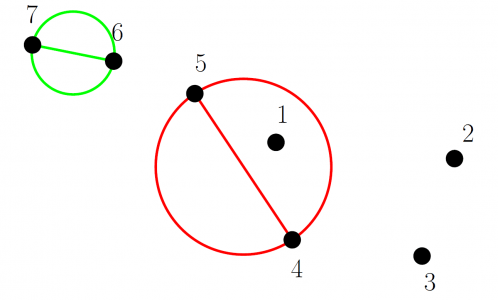
Un día Esther formuló el siguiente problema: “Dados cinco puntos en el plano en posición general (no puede haber tres en la misma línea), hay que demostrar que cuatro de estos puntos forman un cuadrilátero convexo (todos sus ángulos interiores miden menos de 180º).
Esther propuso una sencilla demostración, razonando de este modo: La envolvente convexa (el menor conjunto convexo que los contiene) de cinco puntos en posición general es uno de los tres polígonos siguientes:
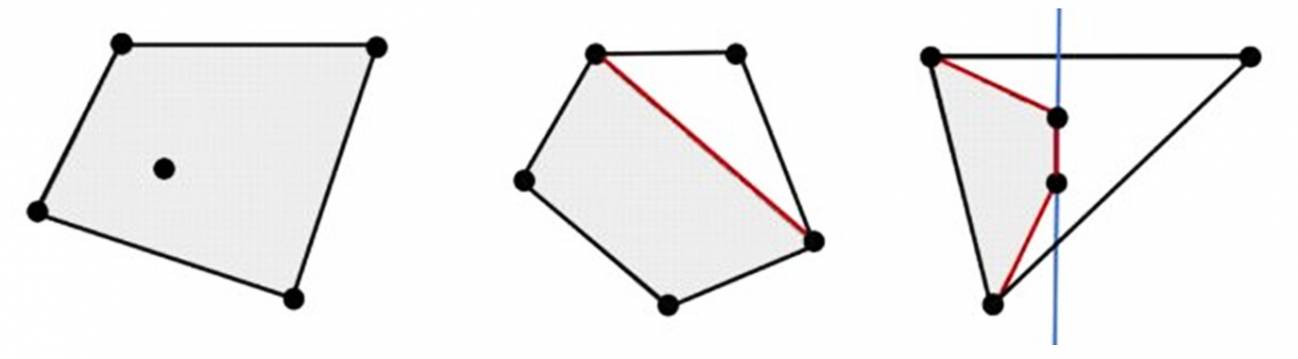
Erdős llamó a este problema “el del final feliz” porque sus dos compañeros, Esther y George se casaron en 1937. Permanecieron unidos durante toda su vida, se trasladaron a Australia tras la Segunda Guerra Mundial y fallecieron justo el mismo día, el 28 de agosto de 2005, con tan solo una hora de diferencia. Ella tenía 95 años y él 94.
Por David Orden, matemático y profesor de la Universidad de Alcalá (Madrid). Basándose en la geometría, ha desarrollado una metodología para facilitar y abaratar las catas de bebidas como el vino o la cerveza, o productos alimentarios como nos enseña aquí.
Participante en una cata de galletas juntando las que considera sensorialmente parecidas. / D. Orden et al./UAH
El entrenamiento de un panel de catadores expertos puede resultar largo y costoso para la industria alimentaria, pero se puede usar un método más rápido y barato: SensoGraph, que permite conocer la opinión de un grupo de consumidores o catadores no entrenados sobre los parecidos y diferencias entre varias muestras. Las opiniones se procesan (con la ayuda de un software sencillo) utilizando técnicas geométricas en lugar de estadísticas.
Por ejemplo, supongamos que queremos analizar varias galletas. En primer lugar cada uno cata todas y coloca cerca las que considera parecidas y lejos las diferentes. Este proceso puede hacerse moviendo imágenes de las galletas en una pantalla o físicamente las galletas sobre un mantel como en la figura de arriba, donde se observa que el catador pone más cerca las galletas que considera más parecidas.
Una vez que se tienen las opiniones de todos los catadores, necesitamos fusionarlas en una sola, para conocer la opinión global del grupo. Para ello SensoGraph utiliza la geometría que se esconde tras las posiciones de las galletas en cada respuesta. Una opción es medir las distancias entre ellas para obtener una tabla, similar a la que suelen incluir los mapas de carretera con las distancias entre ciudades.
Otra posibilidad es unir dos galletas solo cuando no haya una tercera en su área de influencia (por ejemplo, en un círculo con esas dos galletas en los extremos), y se hace una tabla con el número de uniones. Este tipo de tablas nos da la opinión global sobre qué galletas deben estar más cerca y cuáles más lejos.
En este vídeo podemos ver otro ejemplo sobre agregación de países europeos, colocando más cerca los elementos considerados similares y más lejos los distintos. Con un solo clic, el software muestra cómo quedan posicionados según la opinión global de todos los participantes.
De vuelta al ejemplo de las galletas, este método se ha utilizado para estudiar las que tenían pepitas de chocolate en 7 marcas blancas y 1 marca comercial, que se incluyó por duplicado.
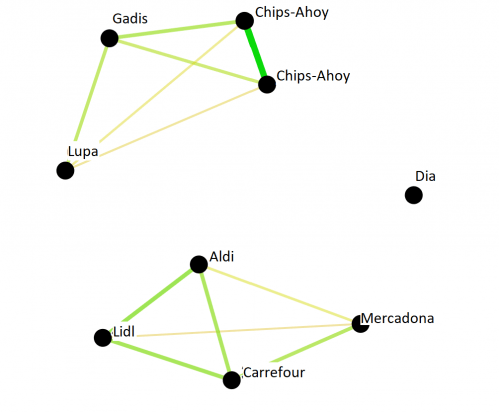
El resultado final muestra las galletas más similares, precisamente las duplicadas, y además permite ver tres grupos claros que indican qué galletas de las de marca blanca se percibieron como más parecidas a las comerciales.
Por Pilar Moreno, profesora de Matemáticas de Secundaria durante 38 años y divulgadora de las matemáticas mediante la fotografía. Entre sus diversas actividades en este ámbito, participa en las exposiciones Geometría Natural y Matemáticas para un mundo mejor en el metro de Bilbao.
‘Traslaciones y simetría’, fotografía de alumnas del IES Benlliure de Valencia. / Pilar Moreno
Hace más de una década que dejó su actividad docente, pero para animar a otros profesores de matemáticas y alumnos a usar las cámaras, Pilar recuerda como trabajaba en sus clases: “El primer paso era aprender y proyectar imágenes sobre conceptos geométricos. Cuando quedaban claros, el reto de los estudiantes consistía en hacer fotografías donde apareciera alguno de esos conceptos”.
Las fotos se comentaban y se discutía sobre ellas en el aula. A veces usaban el ordenador para dibujar con líneas de colores los movimientos geométricos y precisar datos: giro de 120 grados, por ejemplo, simetría axial (donde los puntos de una figura coinciden con los de otra tomando de referencia un eje, como si fuera un espejo), traslación (una transformación geométrica que mueve cada punto de una figura a la misma distancia en una dirección), etc.
“Hay temas muy buenos para trabajar con fotografía, por ejemplo, los cuerpos geométricos, las cónicas o las curvas especiales”, apunta Pilar, “y a los alumnos les cambia la mirada, aprenden a ver lo que tienen alrededor y disfrutan con lo que hacen”.
La veterana profesora ofrece dos ejemplos realizados hace mucho tiempo en la playa por tres de sus alumnas de 4º de ESO (Amanda, Paula y Laura) en el IES Benlliure de Valencia: las fotografías ‘Traslaciones y simetría’ (sobre estas líneas) y ‘Giro en la arena y simetría-asimetría’ (abajo). “Disfruté con sus trabajos tanto como creo que lo hicieron ellas”, rememora Pilar.
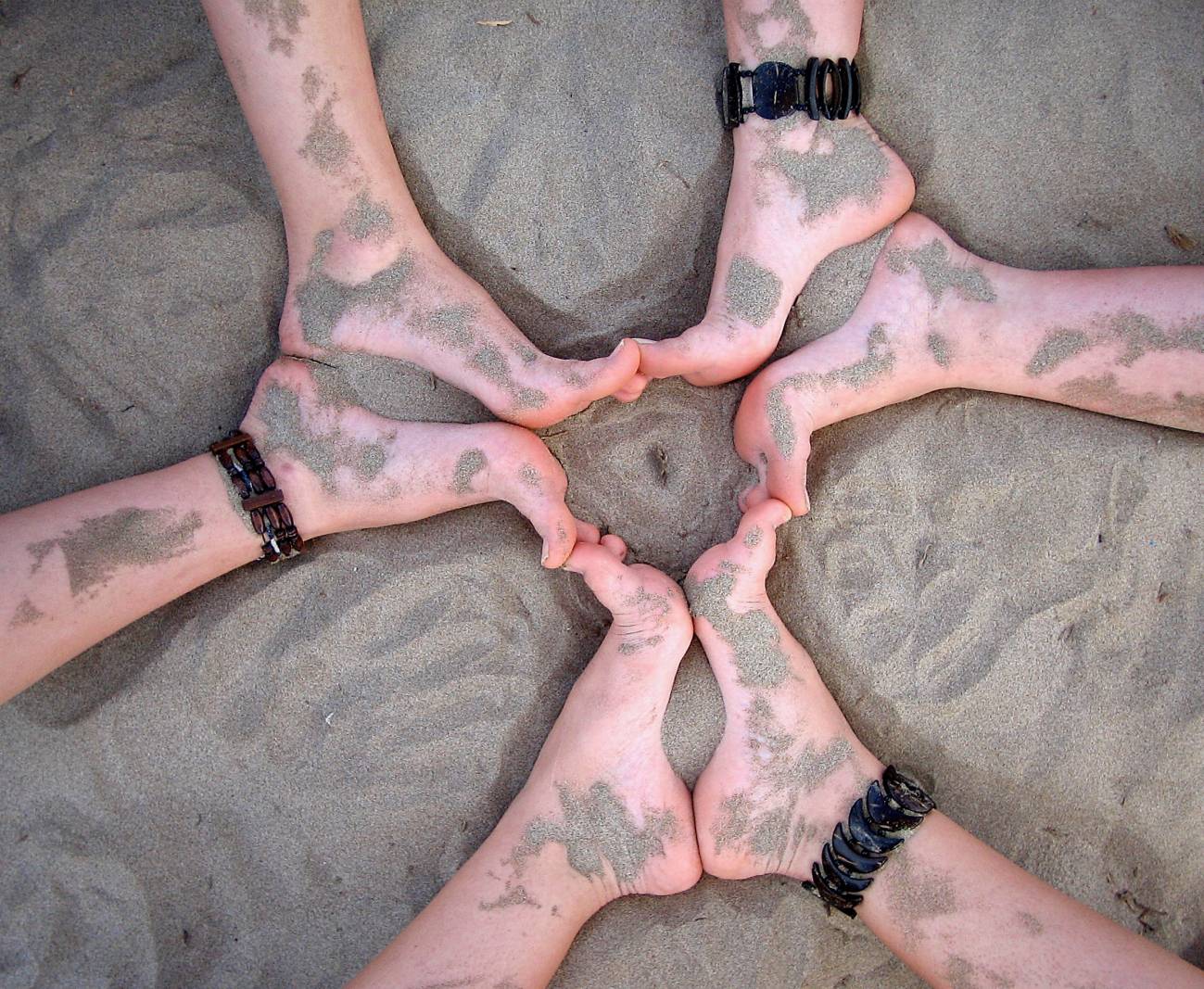
‘Giro en la arena y simetría-asimetría’ / Amanda, Paula y Laura del IES Benlliure de Valencia
La vida es un milagro estadístico. Mientras que las probabilidades de ganar el gordo en el sorteo del 22 de diciembre son de una entre cien mil, el simple hecho de estar vivos supera con creces esa cifra. Esta reflexión nos invita a valorar la extraordinaria suerte de nuestra existencia.
Ecuaciones para modelar el crecimiento de tumores, algoritmos para probar futuras máquinas, avanzadas teorías de computación y una fórmula para marcar un gol son algunos de los temas que se han tratado esta semana en la capital andaluza durante el 9º Congreso Europeo de Matemáticas.
