Los movimientos de las hormigas esconden patrones matemáticos

Los científicos todavía no han descubierto los mecanismos que explican cómo las bandadas de pájaros, los bancos de peces, las hileras de hormigas u otros sistemas naturales complejos se autoorganizan tan bien en sus movimientos colectivos.

Para avanzar en este problema, investigadores de España y EE UU han analizado los movimientos de una hormiga argentina (Linepithema humile, especie invasora en muchas partes del mundo) mientras forrajea o explora un territorio vacío –una placa Petri– y han propuesto un modelo que explica cómo forman sus caminos.

Los autores, que publican su estudio en la revista Mathematical Biosciences, comenzaron observando el comportamiento de las hormigas de forma individual y, posteriormente, de forma colectiva. Registraron todos los movimientos, y a partir de estos experimentos detectaron que los cambios aleatorios en la dirección de los insectos siguen unos patrones matemáticos.

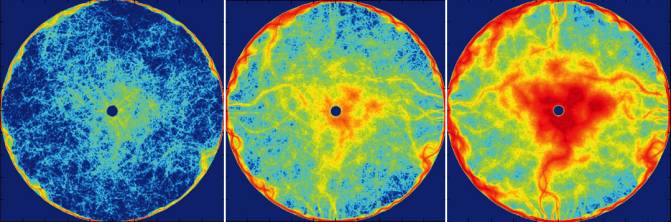
Evolución de la concentración de feromonas tras unos 25 minutos del movimiento de las hormigas. / M. Vela-Pérez, S. Garnier et al.

“En concreto, son una mezcla de distribuciones gaussianas y de Pareto, dos funciones de probabilidad muy usadas en estadística, y que en este caso miden cuanto ‘gira’ la hormiga y hacia dónde en sus desplazamientos”, explica María Vela Pérez, investigadora de la Universidad Europea de Madrid y coautora del trabajo.

Los científicos ya habían comprobado en trabajos anteriores que la ‘persistencia’ de las hormigas, es decir, su tendencia a no cambiar el sentido de su marcha cuando no existen obstáculos o efectos externos, junto al ‘refuerzo’ que se produce en las zonas ya visitadas por el rastro de feromonas que van dejando, son dos factores que determinan las trayectorias de estos insectos durante el forrajeo.

Ahora, con esos datos han podido crear el modelo que describe el movimiento colectivo de las hormigas en el plano. Las simulaciones numéricas en el ordenador muestran la formación de patrones ramificados muy parecidos a los observados en las placas Petri durante el experimento real con las hormigas.

Aparte del mero interés biológico, estos avances podrían aplicarse en diversos campos tecnológicos. “Por ejemplo, se podría usar para diseñar la coordinación de un grupo de pequeños robots para limpiar un área contaminada u otras tareas”, apunta Vela Pérez.

La investigadora recuerda que el estudio de la modelización, organización y coordinación de los comportamientos de los animales es un claro ejemplo de colaboración multidisciplinar, “ya que participan biólogos para realizar los experimentos en el laboratorio y aportar los datos reales, en coordinación con matemáticos y físicos que plantean y resuelven los modelos”.

Uno de los investigadores que ha colaborado en este trabajo, Marco A. Fontelos del Instituto de Ciencias Matemáticas (ICMAT), también es coautor de otro estudio donde se plantea que la formación de hileras de hormigas "se puede caracterizar como bifurcaciones o creación de caminos cuando la concentración de feromonas supera un determinado valor”. Este modelo teórico se basa en ecuaciones en derivadas parciales y los detalles se publican en el Journal of Mathematical Analysis and Applications.